 Quantitative Reasoning is a complex and highly advanced psychometric test. It measures a person’s ability to use mathematical skills in order to solve equations.
Quantitative Reasoning is a complex and highly advanced psychometric test. It measures a person’s ability to use mathematical skills in order to solve equations.
To work in connection with the How2Become Quantitative Reasoning guide, we have provided you with detailed sample questions that takes you step-by-step through the process of working out each type of question.
The important thing to remember is to fully grasp the concept of each question. Once you can apply the methods, you will then be able to use the same method to work out the other questions.
This guide will take you through the process of each question respective of how it is formatted in the Quantitative Reasoning guide.
Quantitative Reasoning – Test Exercise 1
Below are the costs of purchasing land. Prime farmland costs £7,500 per acre. Building land costs £1.1 million per hectare. The table shows the costs, in thousands of pounds per hectare, of cleaning each site. These are paid in addition to the cost of purchasing the land.
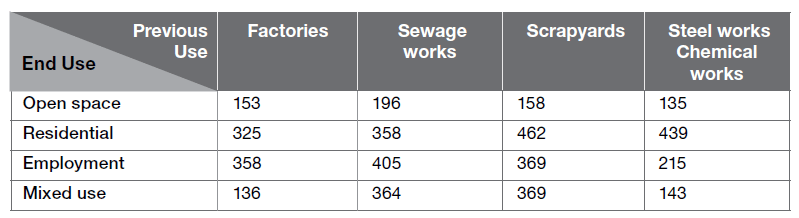
1 hectare = 10,000 m² = 2.47 acres
How many whole hectares of prime farmland could be bought for the total cost of buying one hectare of derelict sewage works and cleaning it for residential use?
How to work it out
Step 1 = first, you need to add the total cost for building on land with how much it costs to build on sewage works for residential use.
1,100,000 + 358,000 = 1,458,000
Step 2 = you now need to divide this by the cost of prime farmland:
1,458,000 ÷ 7,500 = 194.4
Step 3 = now, divide this by how many acres equal 1 hectare (2.47):
194.4 / 2.47 = 78.7 hectares
Answer
78 whole hectares
Quantitative Reasoning – Test Exercise 2
A rugby pitch is 70 m wide and 144 m in length. What is the approximate area of the rugby pitch in hectares?
1 hectare = 10,000 m² = 2.47 acres
How to work it out
Step 1 = you are given the equation that 1 hectare = 10,000 m² = 2.47 acres. This is crucial! In the question, you should look at the units of measurement in order to determine the correct answer.
Step 2 = 70 m x 144 m = 10,080 m²
Step 3 = you know that ‘m²’ can be converted into hectares.
Step 4 = 10,080 m² ÷ 10,000 m² = 1.008 hectares.
Answer
1.008 hectares
Quantitative Reasoning – Test Exercise 3
Below are the costs of purchasing land. Prime farmland costs £7,500 per acre. Building land costs £1.1 million per hectare. The table shows the costs, in thousands of pounds per hectare, of how much it costs to clean the sites. These are paid in addition to the cost of purchasing the land.
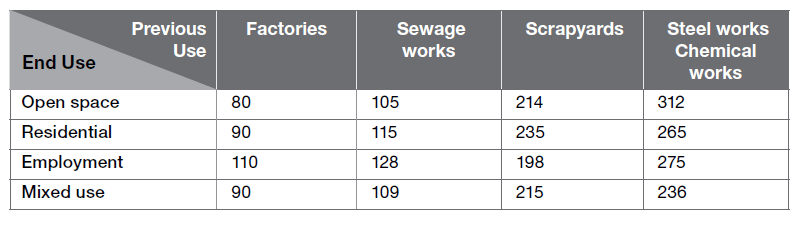
1 hectare = 10,000 m² = 2.47 acres
One of the plots is a square. The diagonal length of the plot is 80 m. Which of the amounts below is closest in value to the cost of buying the plot?
How to work it out
Step 1 = first you need to multiply 80 by 80 to give you an approximate area:
80 x 80 = 6,400
Step 2 = now divide this by 2:
6,400 ÷ 2 = 3,200
Step 3 = divide this by the number of metres squared that equals 1 hectare (10,000)
3,200 ÷ 10,000 = 0.32
Step 4 = multiply this by the price of building land:
0.32 x 1100000 = £352,000
Answer
£352,000
Quantitative Reasoning – Test Exercise 4
A square field, S, has an area greater than 3,600 m². Its length is increased by 10 m, and its width decreased by 10 m to give a rectangular field, R. Which one of the following is true?
A – Area S > area R, perimeter S = perimeter R
B – Area S = area R, perimeter S = perimeter R
C – Area S = area R, perimeter S < perimeter R
D – Area S < area R, perimeter S < perimeter R
E – Area S < area R, perimeter S > perimeter R
How to work it out
Step 1 = to work out these questions, you must have an understanding of what each symbol means
- ‘=’ means to ‘equals’. This could be used in the equation 3 + 5 = 4 + 4. The equals in the middle of the two shows that on each side of the equation, it must equate to the same.
- ‘>’ represents that one number is bigger than the other. A good tip is that the small point of the symbol points to the smaller number, and the large gap represents the bigger number. For example, 8 > 2. This means 8 is bigger than 2.
- ‘<’ represents that one number being smaller than the other. A good tip is that the small point of the symbol points to the smaller number, and the large gap represents the bigger number. For example, 2 < 8. This means 2 is bigger than 8.
Step 2 = you will then need to work out the square root of field S. The square root of 3,600 = 60. (60 x 60 = 3,600)
Step 3 = if the length is increased by 10m, and its width is decreased by 10m, this will give you a field of 70 x 50 (use the width and length from step 2, to increase or decrease each side by the given amount).
Step 4 = now work out the new area of the field by multiply 70 x 50 = 3,500. This is less than that of the first field.
Step 5 = now work out the new perimeter of the field by adding 70 + 70 + 50 + 50 = 240. This has the same perimeter as the first field.
Step 6 = so this can be represented as Area S > area R, perimeter S = perimeter R. In simpler terms, area S is larger than area R, and the perimeter of S is equivalent to perimeter R.
Answer
Area S > area R, perimeter S = perimeter R
Quantitative Reasoning – Test Exercise 5
The following graph shows the velocity of two cars at different times.
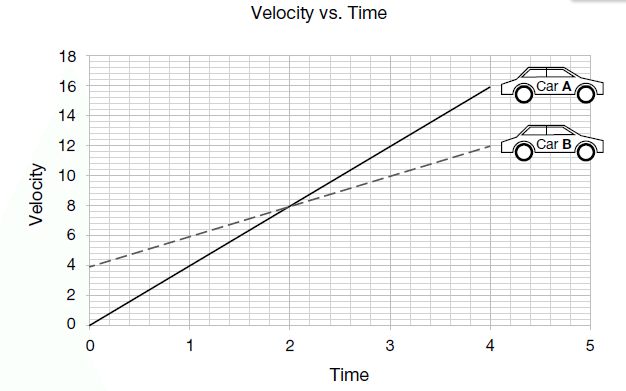
How much greater is the acceleration of Car A than the acceleration of Car B?
Acceleration (m/s2) = change in velocity (m/s2) ÷ change in time (s)
How to work it out
Step 1 = first, you need to work out the acceleration for Car A.
Change in velocity (16 – 0) ÷ change in time (4 – 0)
16 ÷ 4 = 4
Step 2 = now you need to work out the acceleration for Car B.
Change in velocity (12 – 4) ÷ (4 – 0)
8 ÷ 4 = 2
Step 3 = therefore, Car A’s acceleration is greater than Car B’s by 2 m/s2:
4 – 2 = 2 m/s2
Answer
A – 2 m/s2
Quantitative Reasoning – Test Exercise 6
Here is some information about the costs of purchasing land.
Prime farmland costs £6,500 per acre. Building land costs £1.2 million per hectare. The table shows the costs, in thousands of pounds per hectare, of cleaning the sites. These are paid in addition to cost of purchasing the land.
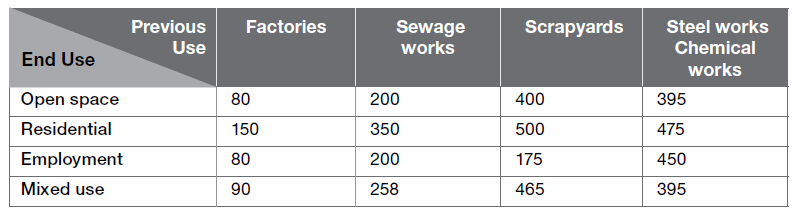
1 hectare = 10,000 m² = 2.47 acres.
Building developers buy an old sewage works with an area of 4 acres. They intend to clean the site for residential use. They know they can use an area 1/10th of an acre for a house. Work out the total cost, to the nearest £, of buying and cleaning the land per house.
How to work it out
Step 1 = first you need to divide the area of acres by how many acres you get for 1 hectare:
4 ÷ 2.47 = 1.619
Step 2 = now, you need to multiply this by 350,000 (the cost for sewage works for residential use + 1,200,000 (cost to build land).
1.619 x (350,000 + 1,200,000)
1.619 x 1,550,000 = 2,509,450
Step 3 = you will then need to use the following method:
2,509,450 ÷ (4 ÷ 10) = 62,736.25
Answer
£62,736.25
Quantitative Reasoning – Test Exercise 7
The following graph shows Ryan’s scores in four projects in his first year at university.
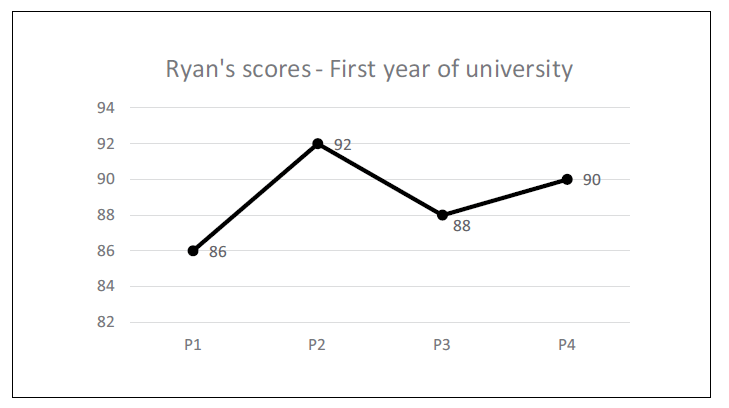
In the second year of university, Ryan scored 88 points in P5. What is the difference between his score in his second year, and his average project score in the first year?
How to work it out
Step 1 = first, you need to work out the average project score of his first year. In order to work out the average, you should add up all of the numbers, and then divide it by how many numbers there are. There are four projects in his first year, so it will be divided by 4.
86 + 92 + 88 + 90 = 356
356 ÷ 4 = 89.
Step 2 = Ryan scores 88 points in P5 (in his second year). Now, you need to work out the difference between his average score across year 1, and the points earned in P5.
89 (average of year 1) – 88 (points scored in P5 = 1
Answer
1
Quantitative Reasoning – Test Exercise 8
Mineral water is classified on the basis of the amount of dissolved solid materials it contains. The chart shows the codes of different levels of total dissolved solids (TDS) and the number of mineral water bottles for each code sold at a store.

What fraction of the total number of bottles sold at the store with TDS greater than or equal to 50 mg/l, have the code TDS 4?
How to work it out
Step 1 = first, you need to work out the bottom number of the fraction. You are trying to work out the total number of bottles sold at the store with TDS greater than or equal to 50, so you need to add up the following:
85 + 65 + 50 = 200 (you add up these numbers because these numbers have TDS 50 or above.
Step 2 = you then to work out the top number of the fraction. You are working out how many bottles have the code TDS 4.
TDS = 50
Step 3 = so the fraction would look like: 50/200
Simplified, this would be 1/4
Answer
1/4
Quantitative Reasoning – Test Exercise 9
The following table shows the percentage of nickel in two coins.
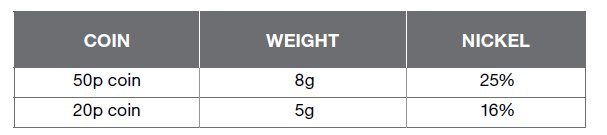
If both coins are made of only nickel and copper, what is the difference between the weight of copper present in the 50 pence coin and the weight of copper in the 20 pence coin?
How to work it out
Step 1 = for the question, you need to work out the difference in copper for both coins, however in the table you are only given the weight and the percentage of nickel.
Step 2 = to work out the weight of copper in the 50p, you know that nickel is equivalent to 25%. That means the weight of the copper will be 75% (there is only two substances: nickel and copper, therefore the rest of the weight must be copper).
8 g ÷ 100 x 75 (weight of copper) = 6 g
Step 3 = to work out the weight of copper in the 20p, you know that nickel is equivalent to 16%. That means the weight of the copper will be 84% (there is only two substances: nickel and copper, therefore the rest of the weight must be copper).
5 g ÷ 100 x 84 = 4.2 g
Step 3 = therefore, the difference between the weight of copper in the 50p and the weight of copper in the 20p would be:
6 – 4.2 = 1.8
Answer
C – 1.8 g
Quantitative Reasoning – Test Exercise 10
The graph shows respondent’s responses when asked what finger they use to type the “Enter” button on the keyboard of a computer.
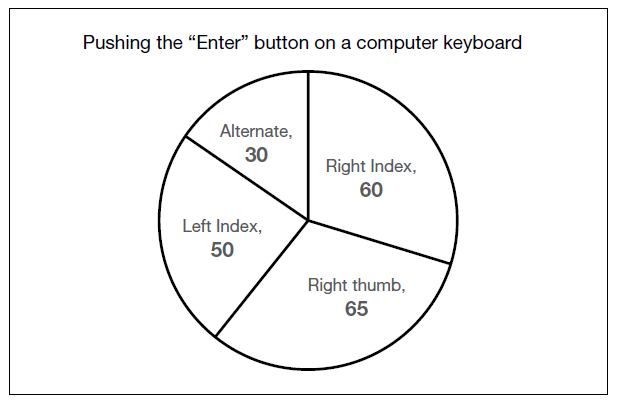
Among all the respondents, only 30% of those who said “Right Index” and 40% of those who said “Alternative” were self-taught typists. How many respondents were self-taught typists?
How to work it out
Step 1 = first, you need to work out 30% of those who said “Right Index”
60 ÷ 100 x 30 = 18
Step 2 = next, you need to work out 40% of those who said “Alternative”
30 ÷ 100 x 40 = 12
Step 3 = now you need to add these two sums up to work out how many respondents were self-taught typists from these categories:
18 + 12 = 30
Answer
30
Quantitative Reasoning – Test Exercise 11
Government spending on “Education services” and “Health services” was 56.3 billion pounds and 106.7 billion respectively for the year 2011-2012. In the same year, Government spending on “Debt interests” was 22.22% of the spending on “Education services”, and the spending on “Education services”, “Health services” and “Debt interests” constituted 50% of the total spending by the Government.
What was the Government’s approximate total spending for the year 2011-2012?
How to work it out
Step 1 = first, you need to work out what the total spending was for “Debt Interests”. You know that this was 22.22% of the spending for Education services which was 56.3 billion.
- 3 ÷ 100 x 22.22 = 12.51 billion.
Step 2 = you then need to add up all of the costs:
56.3 + 106.7 + 12.51 = 175.51 billion pounds.
Step 3 = you know that the above amount (175.51 billion pounds) constituted of 50% of the total spending. So now you need to work out the overall total.
- 51 x 100 ÷ 50 = 351.02 billion pounds.
Step 4 = so the approximate value would be 351 billion pounds.
Answer
351 billion pounds
Quantitative Reasoning – Test Exercise 12
The Siberian tiger population in Country A is 60% of the Siberian tiger population in Country B. The population of Siberian tigers in Country C is 50% of that in Country A.
If the Siberian tiger population in Country C is 420, what is the Siberian tiger population in Country B?
How to work it out
Step 1 = you begin with 420 tigers in Country C. You know that this is 50% of that in Country A. So, to work out Country A, you can use the following method:
420 x 100 ÷ 50 = 840.
Step 2 = you now have 840 tigers in Country A. You know that this is 60% of the tigers in Country B. So, to work out Country B, you can use the following method:
840 x 100 ÷ 60 = 1,400.
So, Country B has 1,400 tigers.
Answer
1,400
Quantitative Reasoning – Test Exercise 13
The following table shows the prices to place different sized advertisements in the main section of a newspaper.
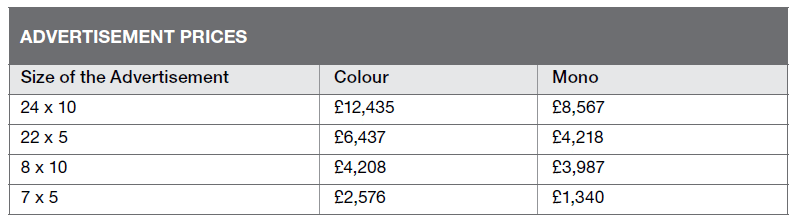
How much more does it cost a company to place two 24 x 10 mono advertisements and one 22 x 5 colour advertisement, as opposed to a company placing orders for three 8 x 10 colour advertisements and one 7 x 5 mono advertisement?
How to work it out
Step 1 = first, you need to work out the total cost for the first company:
Two 24 x 10 mono = 8,567 x 2 = 17,134
One 22 x 5 colour = 6,437.
6,437 + 17,134 = 23,571
Step 2 = next, you need to work out the total cost for the second company:
Three 8 x 10 colour = 4,208 x 3 = 12,624
One 7 x 5 mono = 1,340
1,340 + 12,624 = 13,964
Step 3 = now you need to work out how much more it cost the first company compared to the second company:
23-571 – 13,964 = £9,607
Answer
D – £9,607
Quantitative Reasoning – Test Exercise 14
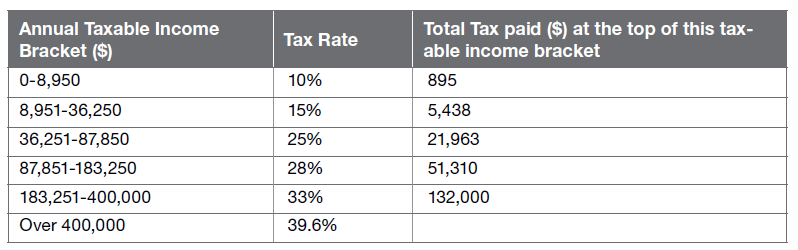
The table shows the total tax paid in $ on annual taxable income.
For example, a person with an annual taxable income of $60,000 will pay $5,438 plus 25% of ($60,000 – $36,251).
Sam has an annual taxable income of $18,500. The income tax, to the nearest $ he has to pay is:
How to work it out
Step 1 = the first step is to work out which bracket Sam’s income falls under. If he earns $18,500, that falls in the 15% bracket.
Step 2 = you need to work out 15% of (18,500 – 8,951). You minus the lowest number of the bracket by the amount.
18,500 – 8,951 = 9,549
15% of 9,549 = 9,549 ÷ 100 x 15 = 1,432.35.
Step 3 = remember you need to add the total tax from the income bracket before. This would be 895 (Sam’s income falls under the second row, so the tax from the first row will need to be added).
895 + 1,432.35 = 2,327.35
Step 4 = to the nearest $, Sam’s total tax would be $2,327
Answer
A – $2,327

Hi, I was struggling with question No. 1 but still after looking at your solution I’m not convinced. Could you explain more in details please? Here is my solution:
step 1: calculation of how much is the price of 1 hectare of Prime farmland
£7,500 x 2.47 = 18,525
Step 2: total costs for building and cleaning sewage land
1100000 + 358000 = 1458000
Step 3: divide this by the price of 1 hectare of Prime farmland
1,458,000 : 18,525 = 78.70
which is wrong!!
I don’t see the reason to divide by the price of 1 acre of Prime farmland since that price express 1 acre, while £1,458,000 is in hectare. Please explain.
Thank you,
regards
Please can you help me solve exercise 21 c example from 11 to 15 the example is 14 ÷ 2 = 10 thank you
Hi Deborah,
Thanks for your comment, we’d be happy to help you. Please could you explain exactly what question you are referring to, so that we can assist you!
Sincerely,
The How2Become Team
Solve exercise 2b for basic 3
Hi Destiny,
Do you want us to solve this question for you? Please let us know if this is the case.
Thanks,
The How2Become Team.
Fatima,
Your way is the correct way. Even I got confused and it took me a whole hour to understand that the third step is wrong.
To convert the total number of acres of prime farmland into number of hectares, one has to divide the result by 2.47 and not multiply it with 2.47.
hence the correct answer is :
194.4/2.47 = 78.70 hectares.
Hi Kunjdeep,
Thanks for your comment. We’ve amended the blog post to reflect the correct answer.
Kind regards,
The How2Become Team.
Hi,
How did you arrive at 408 as the final answer for exercise 1 above?
Thanks.
Hi Ikye,
We’ve amended this blog now to make things clearer, and to reflect the correct answer. Hopefully it all makes more sense to you now, but if you have any questions then please don’t hesitate to get in touch =].
Sincerely,
The How2Become Team